コベルコ科研・技術ノート
こべるにくす
Vol.33
No.60
- TOP
- 技術ノート「こべるにくす」一覧
- アーカイブス
- ギヤの回転系評価技術
Technical
Report
D
ギヤの回転系評価技術
脱炭素化の動きの中で、各自動車メーカーはバッテリー電気自動車(BEV)については小型・軽量・低コスト化が求められ、ギヤの回転系の振動や熱マネジメントの評価技術がますます重要になっている。本稿ではギヤボックスに着目し、下記の2つの予測技術に対する取り組み内容を紹介する。
①ギヤボックスの振動予測技術
ギヤボックスの振動は、加振源(モータ・ギヤなど)が複数存在すること、振動伝達系(シャフト、軸受、カップリング)のが複雑であるため、振動を高精度に予測することが難しい。その課題を解決するため、軸受剛性取得試験を活用したギヤボックスの振動予測の高精度化への取り組みを行った事例について紹介する。
②ギヤボックスの熱流体解析
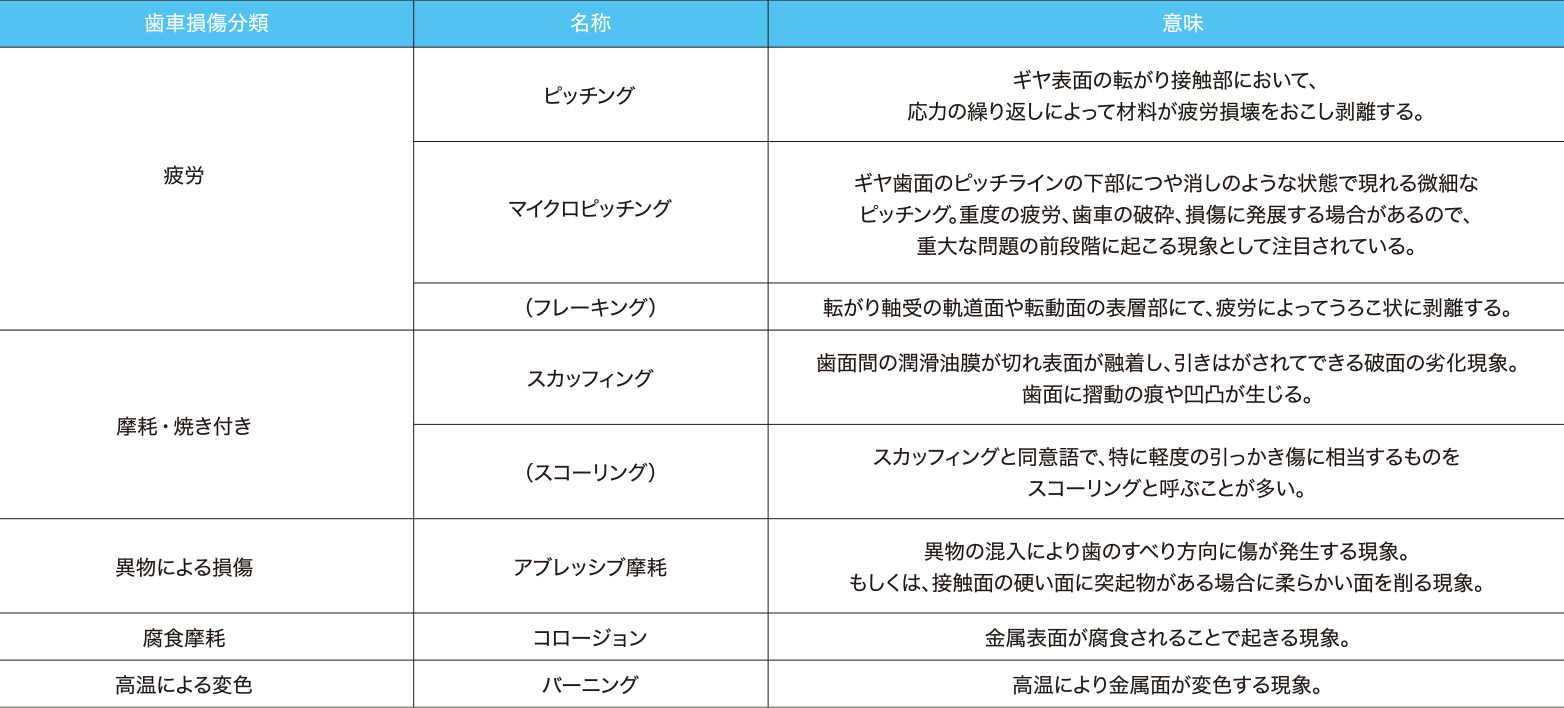
「JISB0160:2015」では、歯面の外観及び歯車に見られる摩耗及び損傷に使用する用語及び定義並びに原因及び対策について規定している。この規格によると、ギヤの損傷分類と名称は第1表のように分類されている。
これらの対策例として、噛み合う歯面間に油膜を形成させることが有効であるとされているが、既往の研究1),2)では、流体潤滑領域で撹拌ロスやスクイーズに着目したものがほとんどであり、潤滑で問題となる混合潤滑領域や境界潤滑領域の摩擦発熱を厳密に表現するものは少なく、この領域でのシミュレーション技術の構築が課題である。そこで、この領域に向けた最初のステップとして、既往の文献と同様の流体潤滑域の熱流体解析に摺動部発熱モデルを組み合わせたモデル構築を行ったので紹介する。
第1表 ギヤの損傷分類と名称
D-1 ギヤボックスの振動予測技術
ギヤボックスの振動伝達系に着目し振動予測の高精度化を図った事例について紹介する。
1.1 軸受剛性取得試験
ギヤボックスのシャフトは一般的には深溝玉軸受、ころ軸受などの軸受で支持される。したがって、シャフトの曲げ振動は軸受剛性による影響を大きく受け、ギヤボックスの振動伝達系のモデル化において軸受剛性を正確に表現することは非常に重要である。深溝玉軸受のラジアル剛性値krは、ラジアル荷重Frに対して式(1)で算出され、ラジアル荷重によって変動する3)。
kr = Cr × 106 × Fr 1/3 B 1/3 N 2/3 cos 5/3 a ( N/m ) ......( 1 )
ここに、Cr=11.76(深溝・アンギュラ玉軸受)
玉径B(m)
ラジアル荷重Fr(N)
転動体の個数N(個)
接触角α(深溝0°,アンギュラ15~40°)
さらに、深溝玉軸受のラジアル剛性は、はめあい公差によってもその剛性が変化することが知られている4)。したがって、式(1)の妥当性を確認するため、はめあい公差を含んだ試験体を製作し、深溝玉軸受の剛性をハンマリング試験により取得した。
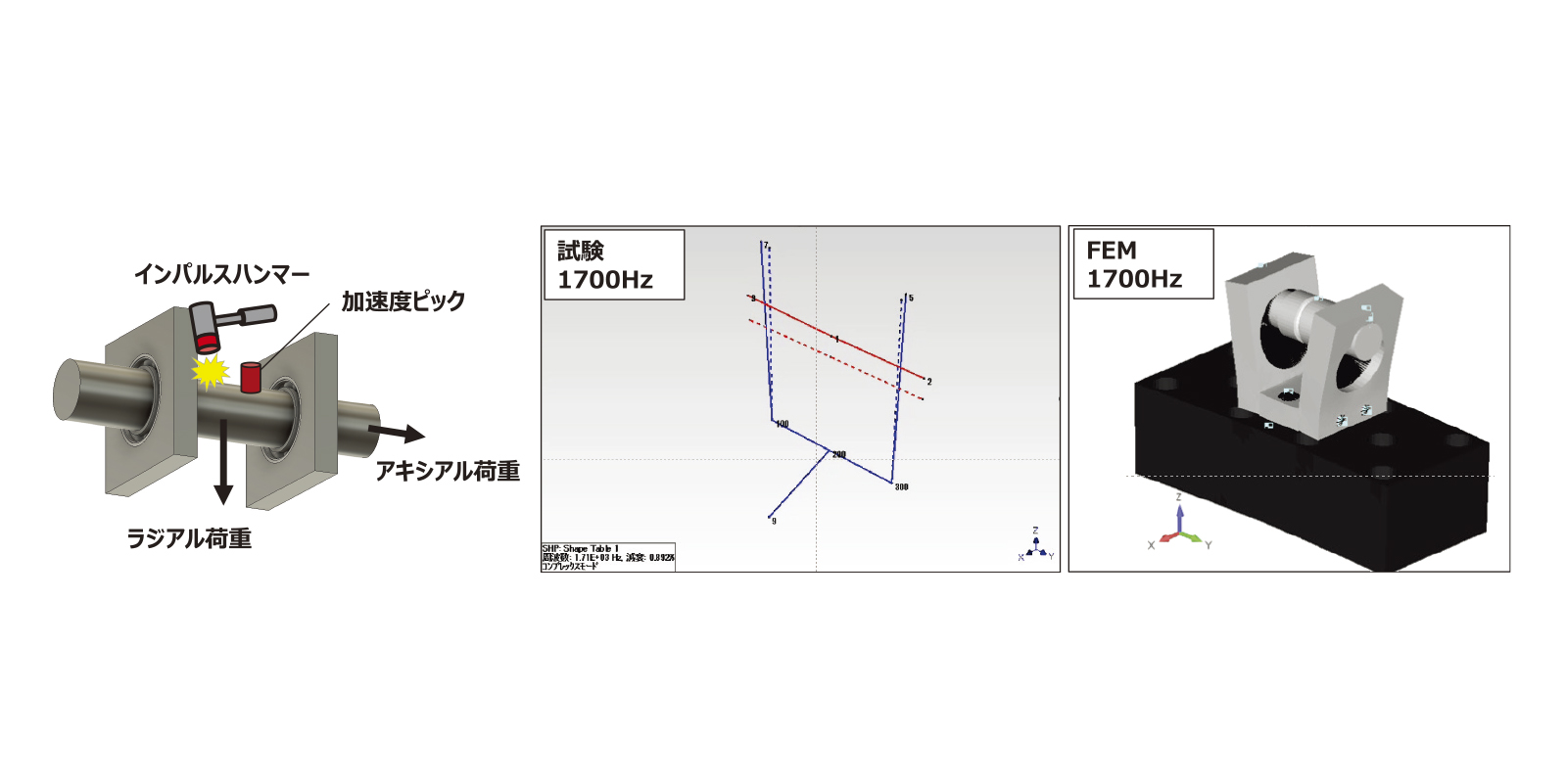
深溝玉軸受のラジアル剛性を取得する試験方法として第1図に示す試験方法を採用した。シャフトの両端を深溝玉軸受で支持し、ラジアルおよびアキシアル荷重を負荷し、共振法により深溝玉軸受のラジアル剛性値を取得した。深溝玉軸受のラジアル剛性はハンマリング試験より求めた共振周波数からFEMを用いて同定した。
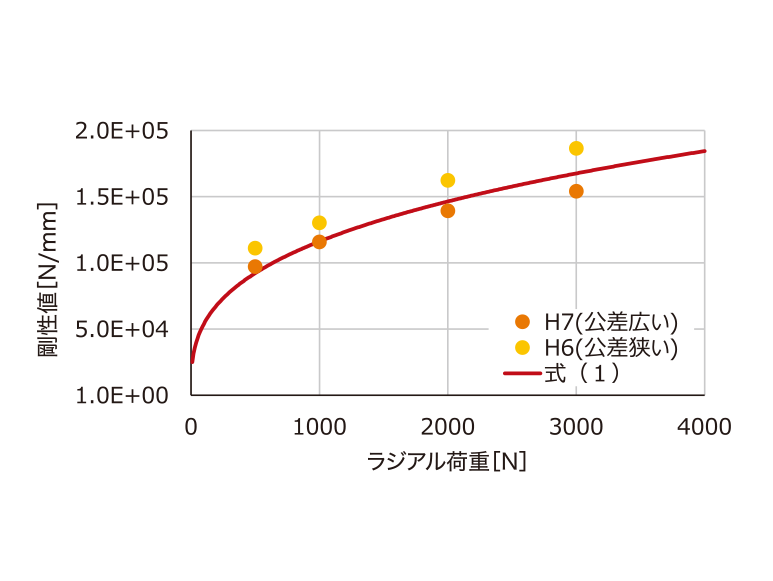
第2図に深溝玉軸受のラジアル剛性値を示す。深溝玉軸受の内輪は「しまりばめ」、外輪は「すきまばめ」とし、はめあい公差は、H7(最大交差+50μm)とH6(最大交差+37μm)の2ケース実施した。式(1)の予測値は試験結果の傾向と概ね一致し試験結果の妥当性が確認できた。また、はめあい公差H7、H6のラジアル剛性値は12から21%の差異があることが分かった。1.2、1.3節で示すギヤボックスはH7で製作したため、H7のラジアル剛性値を用いてFEMモデルを作成した。
第1図 軸受剛性を取得する試験方法
第2図 深溝玉軸受のラジアル剛性値
1.2 ギヤボックスのハンマリング試験とモデル構築
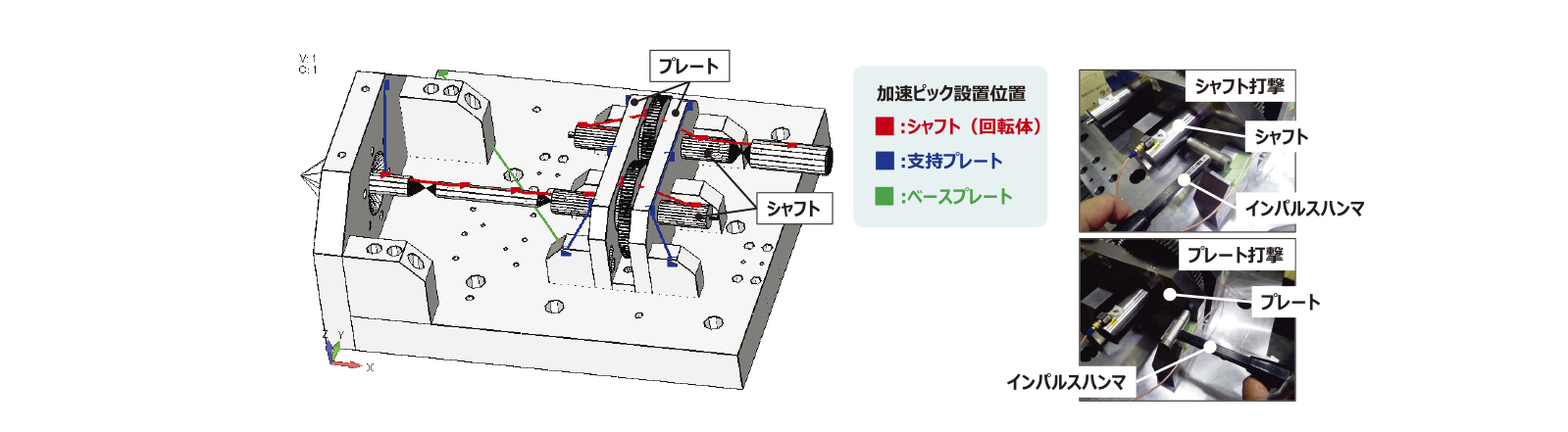
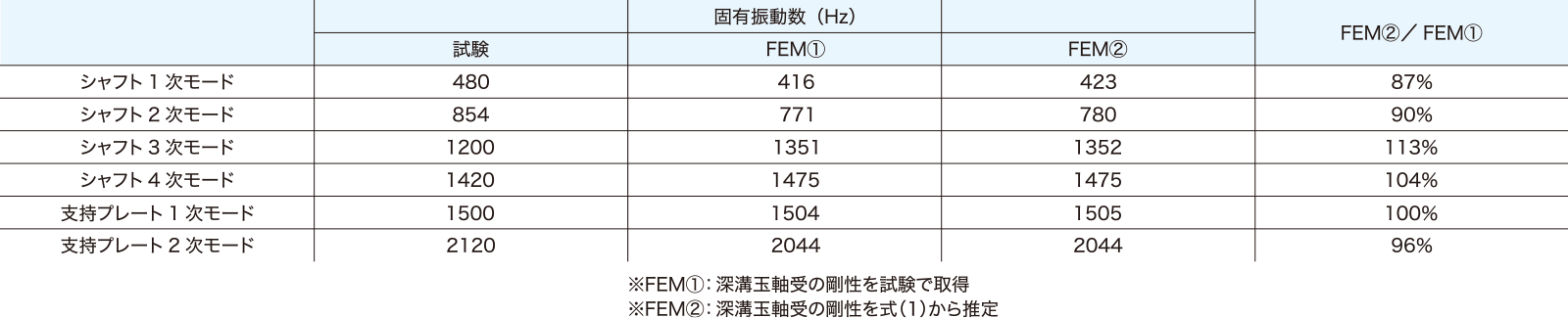
第3図にギヤボックスのハンマリング試験の概要を示す。シャフトおよびプレートをインパルスハンマーで打撃し、シャフトおよびプレートの固有振動数および固有振動モードを取得した。1.1節の軸受剛性試験をもとにFEMモデルを作成し、固有振動数解析を実施した。深溝玉軸受は、はめあい公差H7の試験結果を用いて1Dのばね要素でモデル化した。第4図にシャフトの固有振動モード、第5図にプレートの固有振動モードを示す。シャフトの1次、2次、3次の固有振動数は試験とFEMの差異が少し大きいが、FEMと試験の結果は概ね一致した。第2表に深溝玉軸受のモデル化方法を変更した際の固有振動数の一覧を示す。FEM①は試験から得られた深溝玉軸受の剛性値を用いた結果、FEM②は式(1)の推定値を用いた結果を示す。今回の深溝玉軸受の事例においては、試験から推定した剛性値と式(1)から推定した剛性値の差異が小さく、固有振動数に差がほとんど無かった。したがって、一般的な深溝玉軸受の剛性は式(1)をもちいることで、ハンマリングの試験結果を概ね推定することができると考えられる。また、特殊な形状の軸受を設計に活用する場合には、式(1)が活用できないため、1.1節の計測方法を用いて計測することが有効であると考えられる。
第3図 ギヤボックスのハンマリング試験の概要
第4図 シャフトの固有振動モード
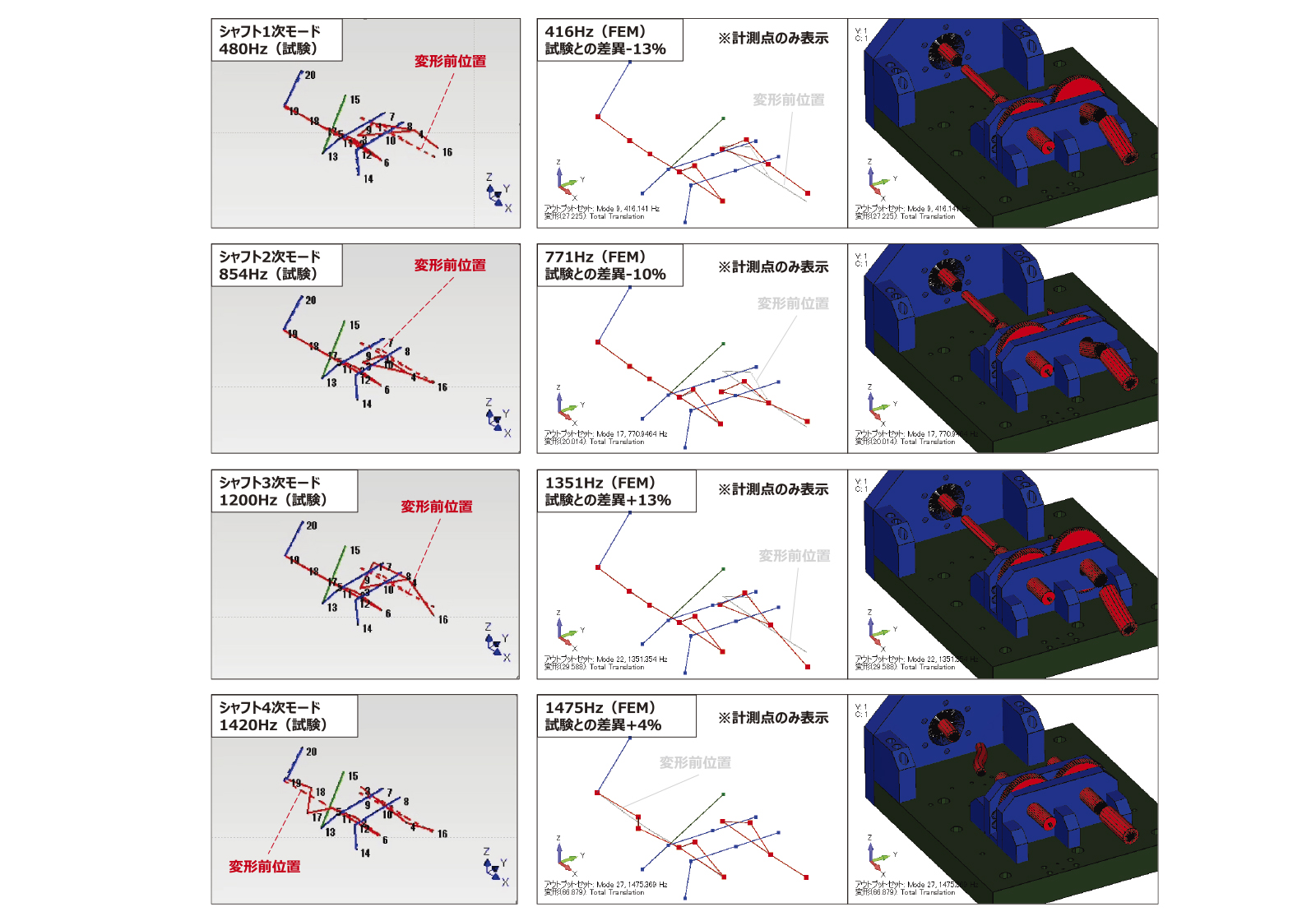
第5図 支持プレートの固有振動モード
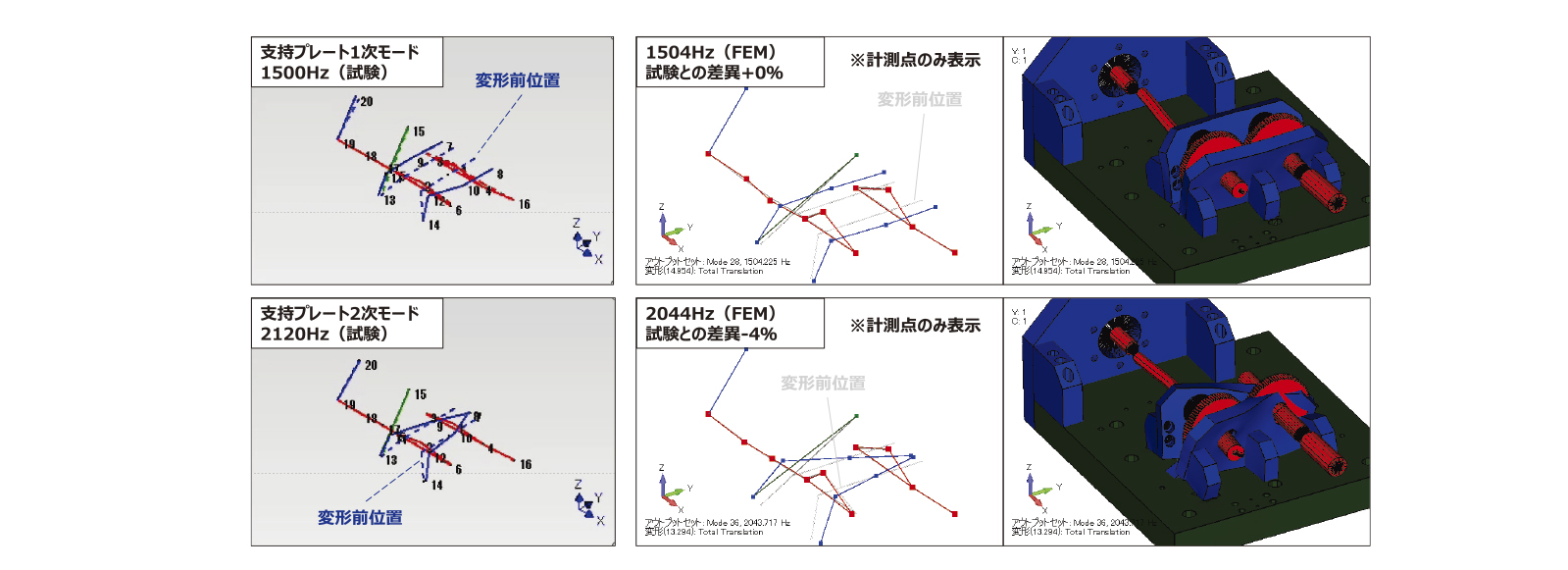
第2表 深溝玉軸受のモデル化方法を変更した際の固有振動数一覧
1.3 ギヤボックスの回転試験とシミュレーション
第6図にギヤボックスの回転試験機を示す。駆動装置にモータを使用し、アウトプット側のシャフトにパウダーブレーキでトルクを負荷した。回転数はインバータで制御した。インプット側およびアウトプット側のシャフトの端面にロータリーエンコーダを設置し、回転数を検出した。また、ギヤボックスの振動は計測点位置の図中赤矢印方向の加速度を計測した。
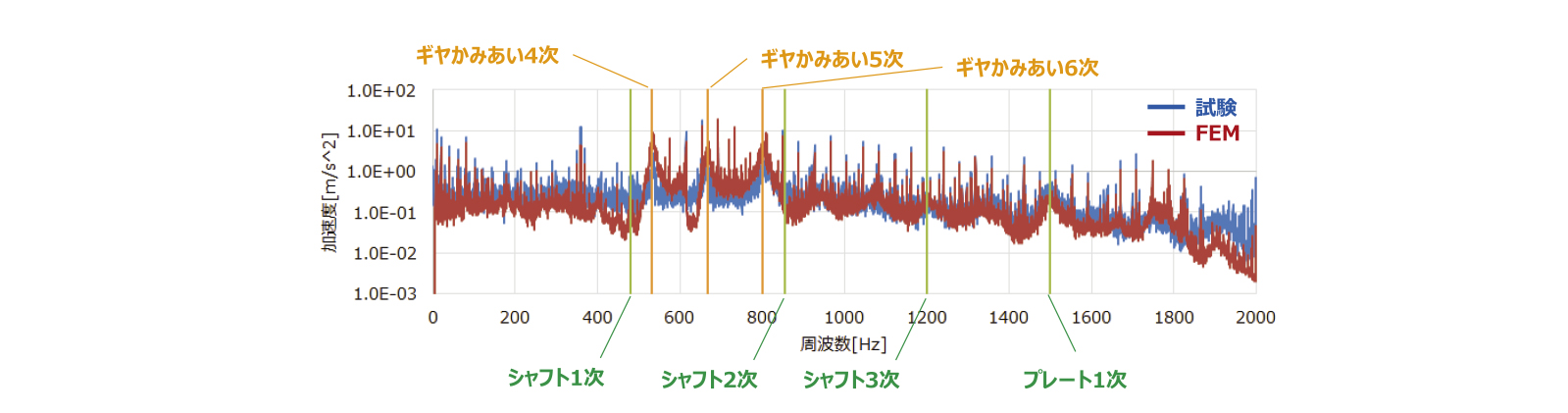
第7図に計測点の加速度の試験結果とシミュレーション結果を比較した結果を示す。ピーク周波数と、ピーク高さの傾向が、1800Hz付近までよく一致した。とくに、ギヤのかみあい周波数4から6次のピークの傾向、シャフト1から3次およびプレートの固有振動数で加速度が大きくなっている傾向が一致した。また、60Hz間隔で発生しているピークはモータのキャリア周波数である。いっぽう、シャフト1次(480Hz)付近の応答値は試験よりFEMが小さくなった。これはシャフト1次の固有振動数が試験とFEMで-13%差異があることが要因であると考えられる。ギヤのかみあい4次の周波数は533Hzであり、その近傍のシャフト1次の固有振動数(試験:480Hz)が励起される。シャフト1次の固有振動数は試験が480Hzであるのに対して、FEMは416Hzである。したがって、480Hz付近のFEMの応答値が小さくなったのは、FEMのシャフト1次の固有振動数が実際より低くなってしまったことで、ギヤのかみあい4次の加振力が励起されにくくなったと考えられる。シャフト1次の固有振動数の再現性を向上させることでさらに予測精度を向上させることができると予想される。具体的な方法としては、モータのシャフトのハンマリングによる境界条件の同定、カップリングの6軸方向の剛性試験などが考えられる。
第6図 ギヤボックスの回転試験

第7図 試験とシミュレーションの比較
D-2 ギヤボックスの熱流体解析
2.1 解析モデル
ギヤの諸元を第3表、解析モデルの外観を第8図に示す。
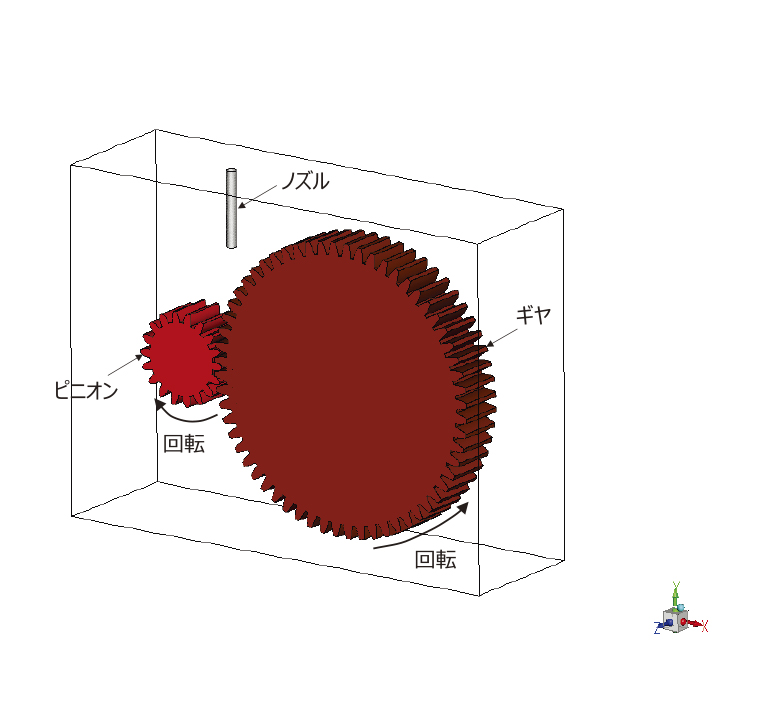
ギヤボックスのサイズは250mm×75mm×h185mmである。このギヤボックス内に1対のギヤを配置した。このとき、液面はピニオンギヤが10mm浸漬する位置に設定した。また、ギヤの接触部に向けてオイルを供給できるようにギヤの中心から60mm離れた位置にノズルを配置した。ギヤの材質はSUS316相当、オイルは一般的なATFとした。
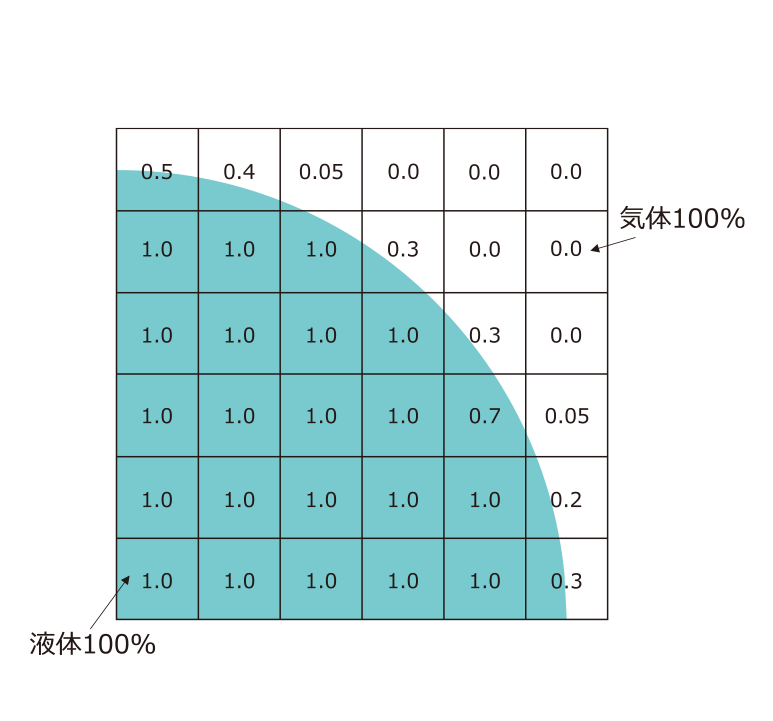
ピニオンは時計回り、ギヤは半時計周りに回転してオイルが撹拌される。このときのオイルの挙動は、VOF(Volume of Fluid)法により気液二相流として表現した。VOF法は気体と液体の混相流解析のうち自由表面流れの解析手法で、第9図に示すように解析メッシュの体積のうち気体と液体の割合を0~1で表す方法である。
ギヤ同士が接触して噛み合うことにより生じる摺動部の瞬間摩擦発熱量は、Long5)らによると式(2)、(3)で表される。
q1 = βγμc PNc VGc × 106 ......(2)
q2 = (1-β) rμc PNc VGc × 106 ......(3)
ここに、β:熱流束の分配定数
γ:熱交換係数(0.95)
μc:摩擦係数
PNc:接触圧力 [Pa]
VGc:すべり速度 [m/s]
これらの式は、Hertzの接触圧、すべり速度、摩擦係数などから導出されている。本稿でも、これと同様に算出した瞬間摩擦発熱量を境界条件として与えた。
また、定常状態のシミュレーションではなくピニオンが1回転する間の温度上昇をシミュレーションした。
第3表 ギヤの諸元

第8図 解析モデルの外観
第9図 VOF法のイメージ図
2.2 解析結果
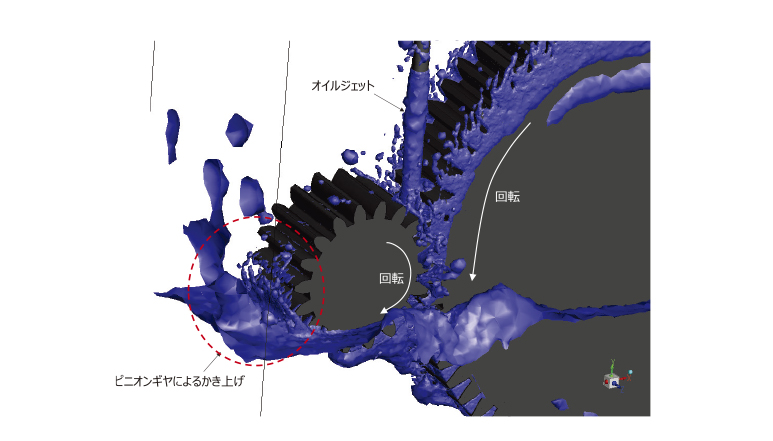
第10図にギヤ近傍のオイル挙動を示す。
気液界面をVOF値で表しており、VOF値=0.5を気液界面として表現した。ここでは、青色が気液界面を表している。
ギヤの噛み合い部にオイルジェットによってオイルが供給されており、ギヤの隙間に入りきらないオイルがギヤの側面からあふれ出ている様子がわかる。ピニオンの回転によりギヤボックスの壁面との間にはオイルがかき上げられて飛散している様子がわかるが、それほど大きくかき上げられていないことがわかる。また、ピニオン上部表面にはオイルがほとんどなく、浸漬だけでは潤滑が不足することが予想される。
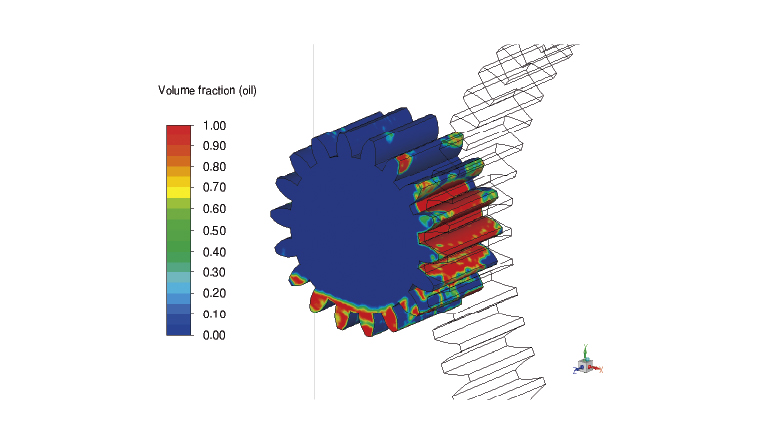
第11図にピニオン表面の潤滑状況を示す。
コンターの0が空気、1がオイルを表している。
噛み合い部にオイルを供給しているため、噛み合い部の歯面は油膜が形成されていることがわかる。第10図でもわかるように、ピニオン上部にはほとんどオイルが無く噛み合い部近傍の歯面で油膜が形成されていることから、オイルジェットは潤滑性への寄与度が高いと考えられる。
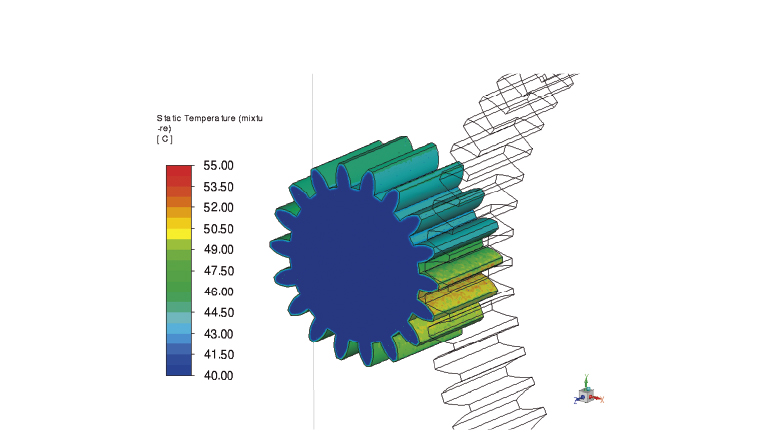
第12図にピニオンの表面温度コンターを示す。
ギヤの噛み合い部手前で約43℃、噛み合い部で約55℃、噛み合い部通過後は約47℃であることがわかる。これは、既報6)と比べると温度は低めであるが、妥当な結果の範囲であると考えられる。ギヤの噛み合い部では、摺動発熱モデルによる発熱とオイル冷却による放熱が同時に起こり、噛み合い部を通過するとオイル冷却のみとなる。したがって、この温度分布はギヤが1回転する間の発熱と放熱の過渡的な状態を表したものである。噛み合い部で発熱するため、最高温度は噛み合い部となり、1回転する間に冷却されるため、最低温度は噛み合い部手前となる。
本稿では定常状態ではないので表面のみが高温となる状態であるが、解析時間を進めると内部にも伝熱して温度上昇すると考えられる。
第10図 ピニオン近傍のオイル挙動
第11図 ピニオン表面のオイル潤滑状況
第12図 ピニオンの表面温度コンター 単位:℃
ギヤボックスの振動予測技術では、振動伝達系に着目し、軸受剛性を計測およびハンマリング試験を活用してFEMで振動加速度を予測した。その結果、ギヤの振動加速度は1kHzを超える高周波域まで精度良く予測することができた。いっぽう、さらなる予測精度向上に向けた改善点も見えてきた。今後は本技術を応用して回転機器の高速化への振動問題の課題解決に活用していく。
ギヤボックスの熱流体解析では、流体潤滑領域のCFDモデルにHertzの接触圧より導出した摺動部発熱モデルを組み合わせたモデルを構築し、ギヤの噛み合いによる温度上昇をシミュレーションすることができた。今後も解析技術の高度化を行い、混合潤滑領域の発熱を厳密にモデル化するなどの課題解決を進め、ギヤの損傷可能性を予測できるようにしていきたい。
参考文献
- *1) FRANCO CONCLI et al.:A CFD analysis of the oil squeezing power losses of a gear pair, Int. J. Comput. Methods Exp. Meas., Vol2(2014), No.2
- *2) Hua Liu et al.: Detailed Investigations on the Oil Flow in Dip-Lubricated Gearboxes by the Finite Volume CFD Method, Lubricants,Vol.6(2018),No.2
- *3) 松下,他 "続 回転機械の振動-実機の振動問題と振動診断",(2012),pp.82-84,コロナ社
- *4) 板谷,"玉軸受の剛性試験と振動特性予測",第409回振動談話会(大阪),(2023)
- *5) H. Long et al. :Operating temperatures of oil-lubricated medium-speed gears: numerical models and experimental results, Proc. Inst. Mech. Eng., Part G: J. Aerosp. Eng., Vol.217(2003), No.2, pp. 87-106
- *6) Yu Dai et al. :Determination of an Optimal Oil Jet Nozzle Layout for Helical Gear Lubrication Mathematical Modeling, Numerical Simulation, and Experimental Validation, Complexity(2020)
